Incompletezza Dei Numeri Razionali, Incompletezza Di Q
Per fissare le idee consideriamo i due insiemi sono due insiemi separati, infatti per ogni e per ogni. Poiché la condizione è più forte rispetto ad, sussistono le ipotesi dell'assioma di completezza. L'assioma di completezza assicura quindi l'esistenza di almeno un numero reale che si interpone tra gli elementi dell'insieme e gli elementi dell'insieme. In questo caso gli elementi separatori sono infiniti, infatti ogni numero reale appartenente all' intervallo soddisfa la doppia disuaglianza. Unicità dell'elemento separatore Come risulta evidente dal precedente esempio, l'elemento separatore di cui parla l'assioma di completezza in generale non è unico, ma esistono due casi in cui lo è. 1) Se è un insieme non vuoto limitato superiormente e scegliamo come l'insieme dei maggioranti di, allora l'elemento separatore tra e è unico. Ogni elemento separatore deve, infatti, soddisfare la relazione per ogni e per ogni La prima disuguaglianza ci dice che è un maggiorante per, quindi. La seconda disuguaglianza, assieme al fatto che, ci permette di asserire che è il minimo dell'insieme.
Assioma di completezza
Poiché ogni successione di Cauchy è limitata, è non vuoto e superiormente limitato ed ammette quindi, per l'assioma di Dedekind, un estremo superiore. Mostriamo che effettivamente la successione tende a. Per ogni, esiste un tale che per ogni, maggiore o uguale a. Allora la successione assume infinite volte valori all'interno dell'intervallo e un numero finito di volte nel suo complementare. Quindi è un elemento di e è maggiore di ogni elemento di, e quindi è maggiore o uguale ad. Quindi è contenuto nell'intervallo, e per la disuguaglianza triangolare risulta che. Quindi e la successione converge. Q. E. D.
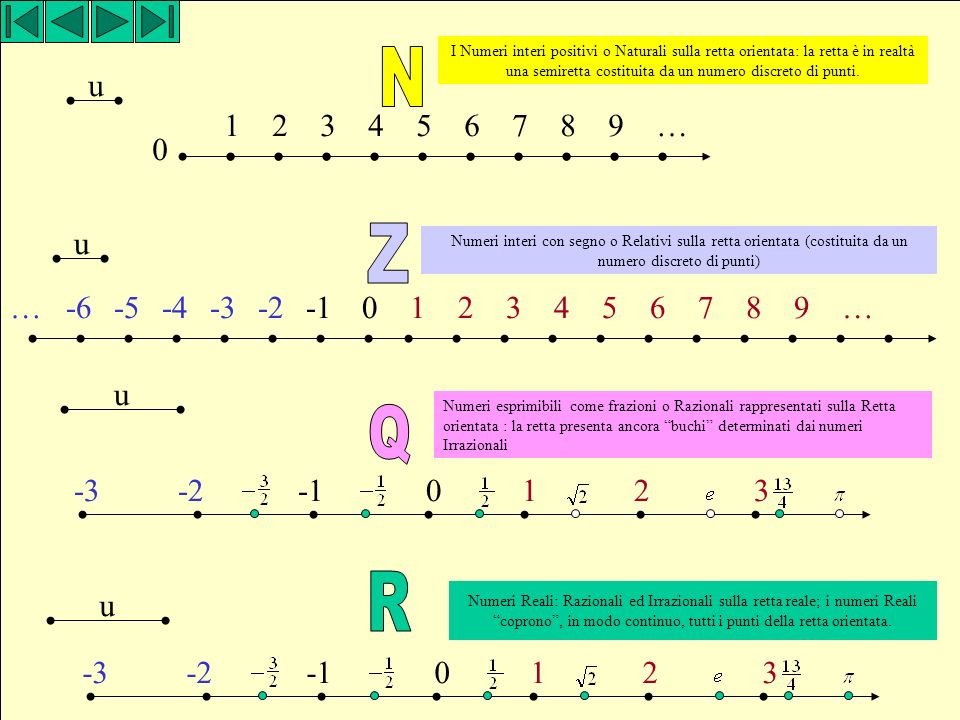
L' assioma di completezza, detto anche assioma di continuità, stabilisce che i numeri reali si susseguono con continuità, ossia che l' insieme R dei numeri reali è "privo di buchi". L'assioma di completezza assume un ruolo fondamentale in Analisi Matematica, per diversi motivi: - insieme ad altri assiomi e proprietà permette di dare una definizione assiomatica dell'insieme dei numeri reali, ossia darne una definizione rigorosa limitandosi a specificare le proprietà che lo caratterizzano; - è l'unica proprietà che differenzia l'insieme R dei numeri reali dall' insieme Q dai numeri razionali; - permette di mettere in relazione l'insieme dei numeri reali con i punti di una retta. Enunciato dell'assioma di completezza Se e sono due sottoinsiemi non vuoti dell'insieme, tali che per ogni e per ogni, allora esiste un elemento tale che per ogni e per ogni L'elemento è detto elemento separatore degli insiemi e e, in generale, non è unico. Sebbene a una prima lettura possa sembrare di difficile comprensione, l'assioma di completezza è un enunciato di tipo esistenziale, ossia si limita ad assicurare l'esistenza di un elemento separatore tra due insiemi separati.
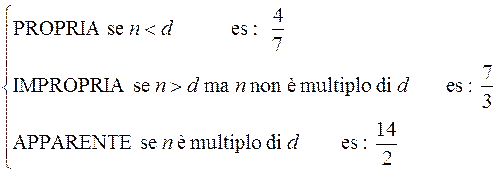
*** Con questo è tutto! Per qualsiasi tipo di approfondimento sull'insieme dei numeri reali vi rimandiamo alla lezione del link, se invece volete sapere cos'è un assioma - click!
De la
Attenzione qui! Potrebbe sembrare un controsenso, ma non è così! Ad esempio: 2d) Se hanno numeratore e denominatore diversi, allora dobbiamo ricondurre le due frazioni allo stesso denominatore (facendo il minimo comune multiplo fra i denominatori) e si confrontano come al punto 2b). A titolo di esempio confrontiamo le frazioni. Calcoliamo il minimo comune multiplo dei denominatori in modo da ridurle allo stesso denominatore Quindi: Essendo 45 maggiore di 14, si ha che. Numeri razionali e numeri naturali Curiosità: è un numero razionale? All'apparenza sembrerebbe di sì, in quanto è una frazione. Se però la riduciamo ai minimi termini (dividendo numeratore e denominatore per 2) otteniamo che è un numero naturale! Quindi? Qual è la risposta giusta alla domanda? Per rispondere correttamente, basta sapere che l'insieme dei numeri naturali è un sottoinsieme dei numeri razionali. Per fissare meglio le idee basta ricordare il seguente diagramma di Eulero-Venn: che ci fa vedere e capire come tutti i numeri naturali sono particolari tipi di numeri razionali!
- Film con cicciolina
- Incompletezza dei numeri razionali 2017
- Incompletezza dei numeri razionali de la
- Incompletezza dei numeri razionali online
- Incompletezza dei numeri razionali 1
- Sondaggi foresta d'opinioni
- Divano
- Misurare la distanza tra due punti - Visio
- Incompletezza dei numeri razionali letra
Da Wikipedia, l'enciclopedia libera. In matematica, l' assioma di Dedekind, detto anche assioma di continuità oppure assioma di completezza, riguarda l'insieme dei numeri reali R; esso afferma che ogni insieme S di numeri reali che non sia vuoto e che sia limitato superiormente possiede un estremo superiore, vale a dire un numero reale uguale o maggiore di tutti gli elementi di S e tale che non esista nessun reale più piccolo con tale proprietà. Se ad esempio l'insieme S considerato è quello dei numeri il cui quadrato è inferiore a 2 (in simboli, l'insieme), l'estremo superiore è. L'assioma si può enunciare anche per ogni sottoinsieme di R che sia non vuoto e inferiormente limitato: in questo caso si garantisce che l'insieme abbia un estremo inferiore. Questo assioma è molto utile perché è essenziale per dimostrare che la retta reale è uno spazio metrico completo. L'insieme dei numeri razionali non soddisfa questo assioma, e perciò non è completo: per l'insieme S definito precedentemente non esiste un estremo superiore appartenente a Q.
Poichè il minimo di un insieme è unico, unico sarà l'elemento separatore. 2) In modo analogo si dimostra che se è un insieme non vuoto e limitato inferiormente e è l' insieme dei minoranti di allora il massimo dell'insieme è l'unico elemento separatore tra e. 3) [Caso generale] Possiamo riassumere i casi 1) e 2) asserendo che due insiemi contigui ammettono sempre un unico elemento separatore. Assioma di completezza in Q Nell'insieme dei numeri razionali non vale l'assioma di completezza e per convincersene basta considerare gli insiemi Ogni elemento dell'insieme è minore di ogni elemento dell'insieme, quindi i due insiemi sono separati. L'unico elemento separatore sarebbe, ma la radice quadrata di 2 non è un numero razionale, quindi non esiste alcun numero tale che per ogni e per ogni. Ciò basta a concludere che l'assioma di completezza non vale nell'insieme e, tra l'altro, è l'unica caratteristica che distingue i due insiemi dei numeri reali e dei numeri razionali: è continuo, mentre non lo è.
Assioma di completezza e continuità della retta [ modifica | modifica wikitesto] Una formulazione alternativa dell'assioma di Dedekind, nota sotto il nome di assioma di completezza, è la seguente. «Presa comunque una partizione di tutti i punti di una retta in due sottoinsiemi, tale che nessun punto di un sottoinsieme giace tra due punti dell'altro, esiste un punto di un sottoinsieme che giace tra tutti gli altri punti di quel sottoinsieme e tutti i punti dell'altro. » L'assioma di Dedekind (o di completezza) permette di porre in corrispondenza biunivoca i punti di una retta con gli elementi dell'insieme R. Completezza dei numeri reali [ modifica | modifica wikitesto] Usando l'assioma di Dedekind si può dimostrare che i numeri reali formano uno spazio completo: in altre parole, che ogni successione di Cauchy è convergente. Dimostrazione [ modifica | modifica wikitesto] Sia una successione di Cauchy. Sia l'insieme dei numeri reali che sono maggiori di solo per un numero finito di valori di.
Se ancora non fosse chiaro, per convincersi di ciò, basta pensare ad un qualsiasi numero naturale. Considera ad esempio 5 e prova a ridurre ai minimi termini: Come risultato otterrete sempre 5. Per approfondire, potete leggere l'articolo sui tipi di frazioni in cui si parla delle frazioni apparenti. È tutto! In una delle lezioni successive parleremo di un altro particolare insieme numerico, quello dei numeri irrazionali, mentre in un approfondimento a parte abbiamo spiegato quali sono le proprietà più o meno avanzate dell' insieme Q. Prima di salutarvi vi consigliamo di consultare le tonnellate di esercizi disponibili su YouMath, usando la barra di ricerca presente in cima ad ogni pagina; e in caso di dubbi o perplessità, non disperate e posta la tua domanda nel Forum. ;) Buona Matematica a tutti, Giuseppe Carichino (Galois)..... Tags: numeri razionali e frazioni - confronto tra numeri razionali.